RECENT RESEARCH WORKS:
Stabilizer-Accelerated Quantum Many-Body Ground-State Estimation
C. E. P. Robin |
arXiv:2505.02923 [quant-ph] (2025)
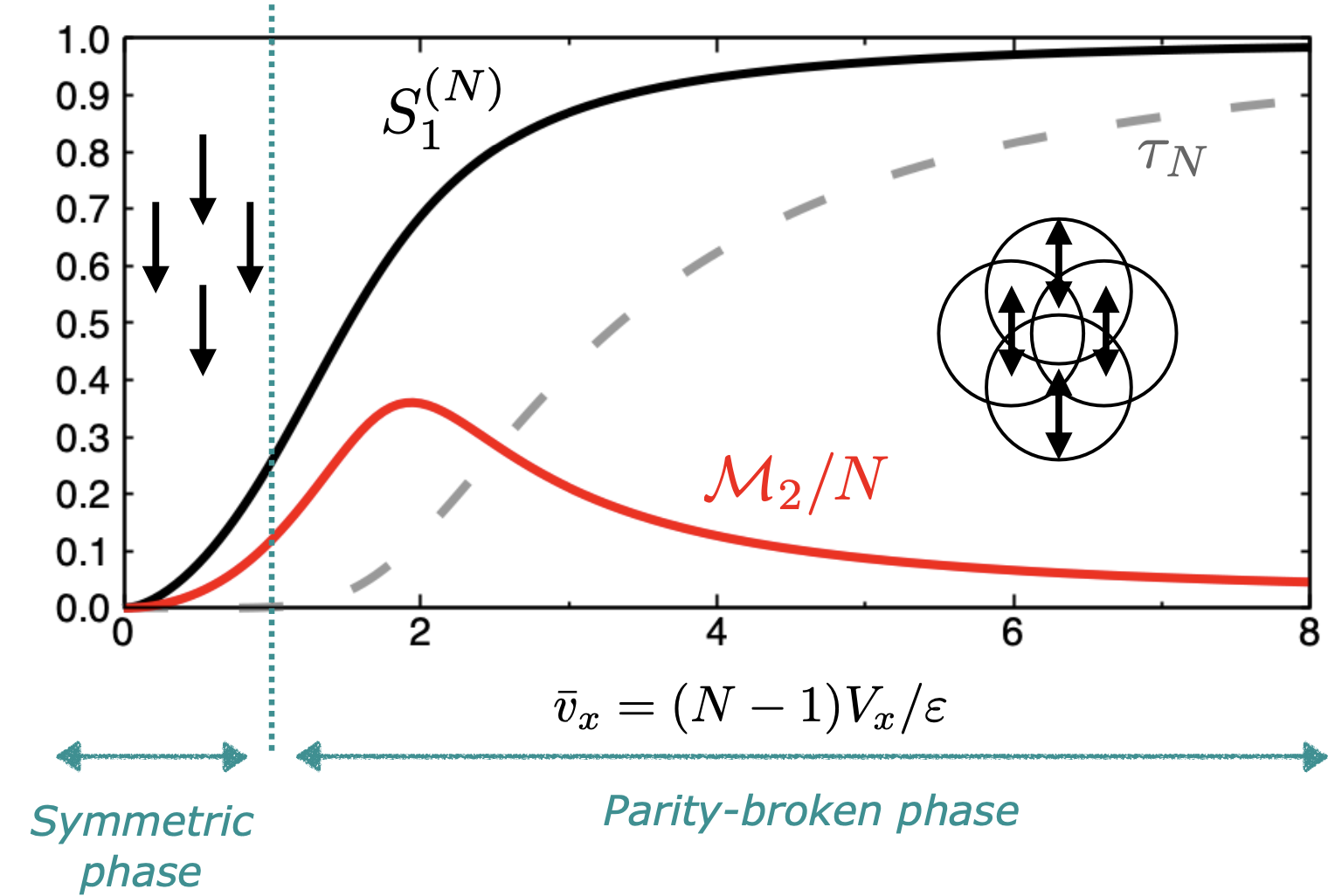
We investigate the use of stabilizer states to describe the emergence of many-body (shape) collectivity from individual constituents, in a symmetry-preserving and classically efficient way.
The method that we adopt is based on
determining an optimal separation of the Hamiltonian into a stabilizer component and a residual part inducing non-stabilizerness. The corresponding stabilizer ground state is efficiently prepared using techniques of graph states and stabilizer tableaux.
While further studies will be needed, this work suggests that collectivity may be associated with high but simple large-scale entanglement which can be captured by stabilizer states, while the interplay with single-particle motion may be responsible for inducing non-stabilizerness.
Quantum Magic and Computational Complexity in the Neutrino Sector
I. Chernyshev, C. E. P. Robin and M. J. Savage |
arXiv:2409.12064 [nucl-th] (2024), Phys. Rev. Res. 7, 023228 (2025).
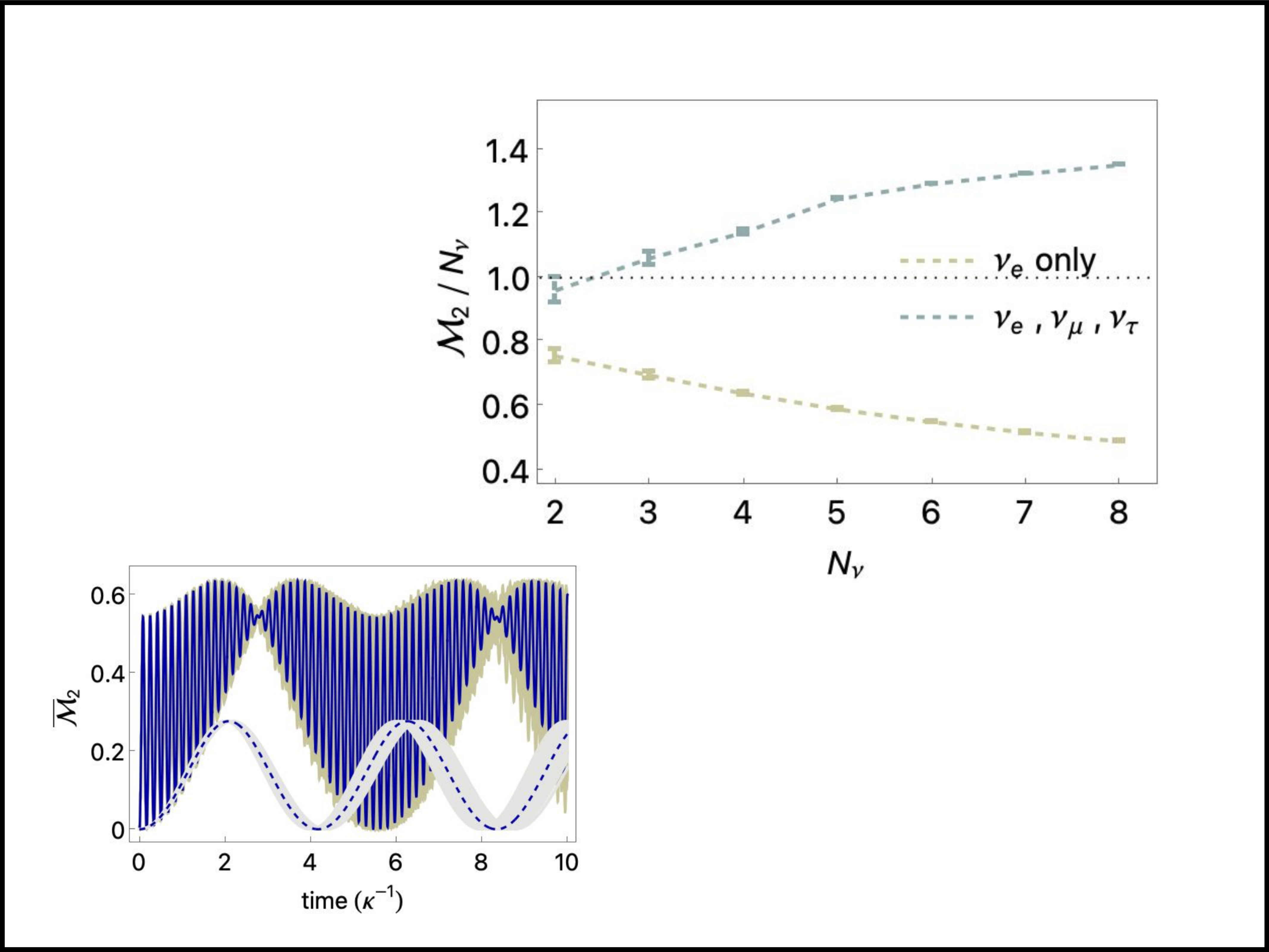
We consider the quantum magic in systems of dense neutrinos undergoing coherent flavor transformations, relevant for supernova and neutron-star binary mergers. Mapping the three-flavor-neutrino system to qutrits, the evolution of quantum magic is explored in the single scattering angle limit for a selection of initial tensor-product pure states for up to 8 neutrinos. For initial states with only electron neutrinos, the magic, as measured by the 2-Rényi entropy, is found to decrease with radial distance from the neutrino sphere, reaching a value that lies below the maximum for tensor-product qutrit states. Further, the asymptotic magic per neutrino decreases with increasing neutrino number. In contrast, the magic evolving from states containing all three flavors reaches values only possible with entanglement, with the asymptotic magic per neutrino increasing with system size.
These results highlight the connection between the complexity in simulating quantum physical systems and the parameters of the Standard Model.
Quantum Magic and Multi-Partite Entanglement in the Structure of Nuclei
F. Brökemeier, S. M. Hengstenberg, J. W. Keeble, C. E. P. Robin, F. Rocco and M. J. Savage |
arXiv:2409.12064 [nucl-th] (2024), Phys. Rev. C 111, 034317 (2025).
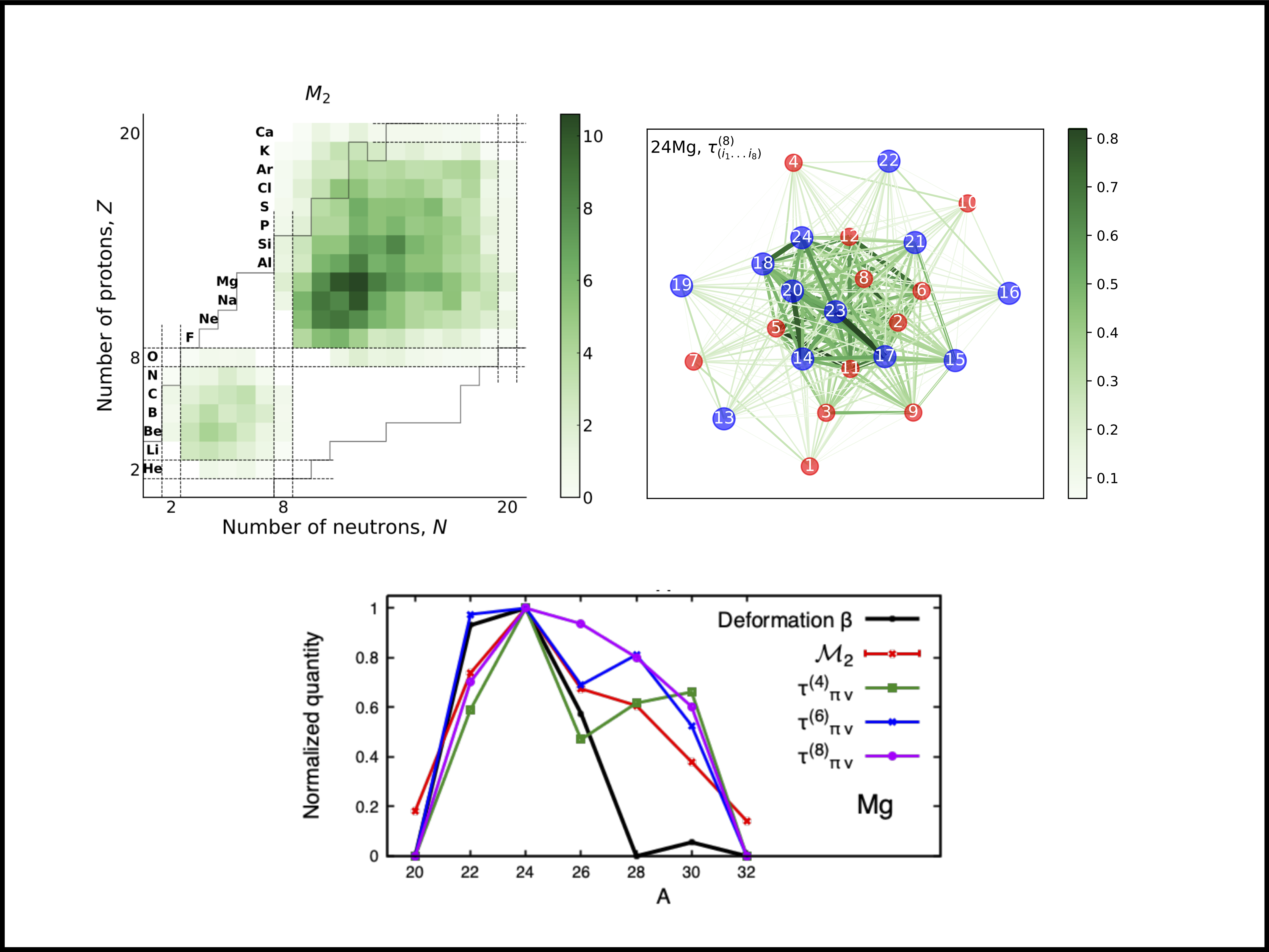
Motivated by the Gottesman-Knill theorem, we present a detailed study of the quantum complexity of
p-shell and sd-shell nuclei. Valence-space nuclear shell-model wavefunctions
generated by the BIGSTICK code are mapped to qubit registers using the
Jordan-Wigner mapping (12 qubits for the p-shell and 24 qubits for the
sd-shell), from which measures of the many-body entanglement (n-tangles) and
magic (non-stabilizerness) are determined. While exact evaluations of these
measures are possible for nuclei with a modest number of active nucleons,
Monte Carlo simulations are required for the more complex nuclei. The
broadly-applicable Pauli-String IZ exact (PSIZe-) MCMC technique is introduced
to accelerate the evaluation of measures of magic in deformed nuclei (with
hierarchical wavefunctions), by factors of 8 for some nuclei. Significant
multi-nucleon entanglement is found in the sd-shell, dominated by
proton-neutron configurations, along with significant measures of magic. This
is evident not only for the deformed states, but also for nuclei on the path
to instability via regions of shape coexistence and level inversion. These
results indicate that quantum-computing resources will accelerate precision
simulations of such nuclei and beyond.
The Magic in Nuclear and Hypernuclear Forces
Caroline Robin and Martin Savage |
arXiv:2405.10268 [nucl-th] (2024)
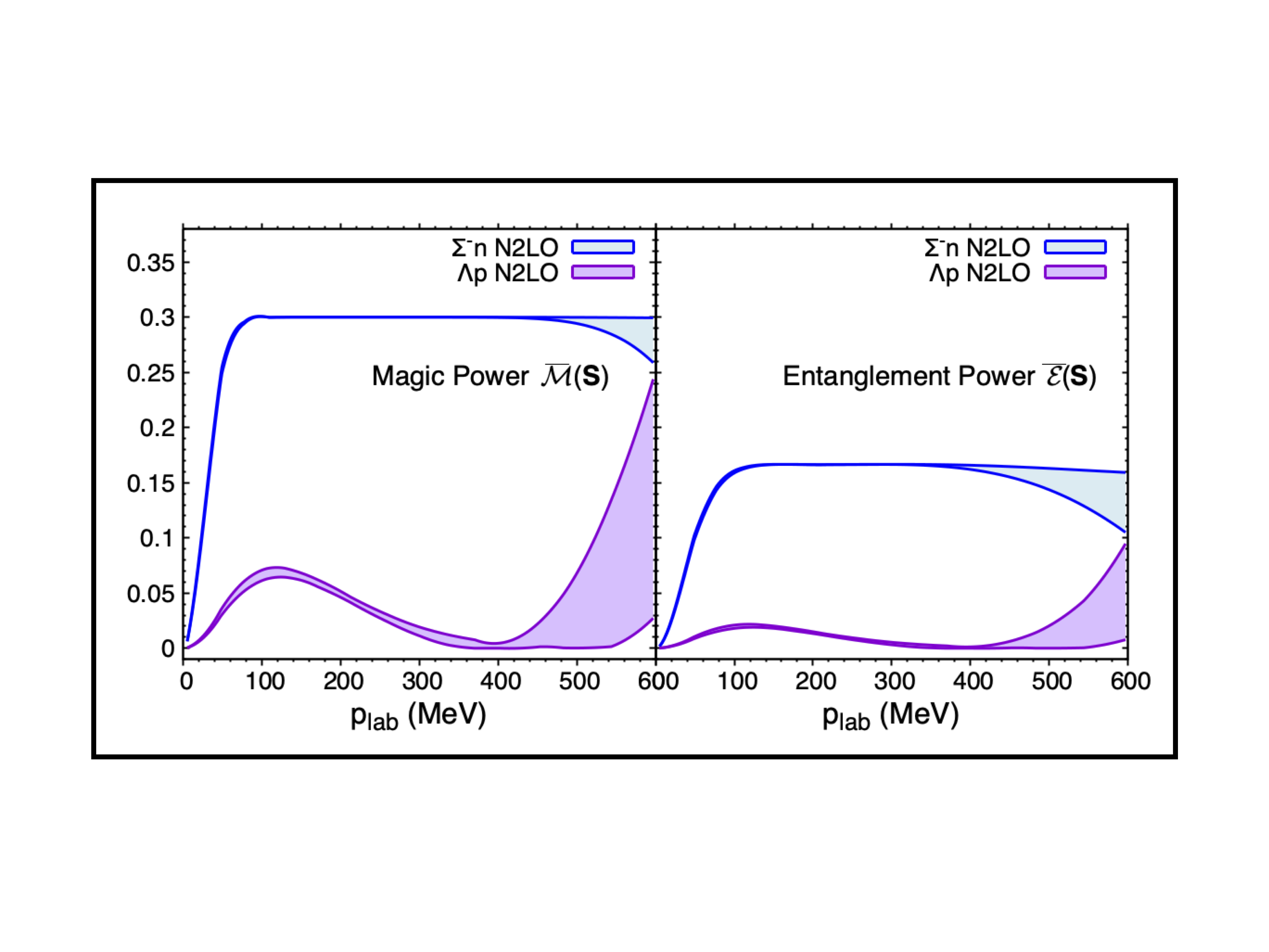
Toward an improved understanding of the role of quantum information in nuclei and exotic matter, we examine the magic (non-stabilizerness) in low-energy strong interaction processes. As stabilizer states can be prepared efficiently using classical computers, and include classes of entangled states, it is magic and fluctuations in magic, along with entanglement, that determine resource requirements for quantum simulations. As a measure of fluctuations in magic induced by scattering, the "magic power" of the S-matrix is introduced. Using experimentally-determined scattering phase shifts and mixing parameters, the magic power in nucleon-nucleon and hyperon-nucleon scattering, along with the magic in the deuteron, are found to exhibit interesting features. The Σ- baryon is identified as a potential candidate catalyst for enhanced spreading of magic and entanglement in dense matter, depending on in-medium decoherence.
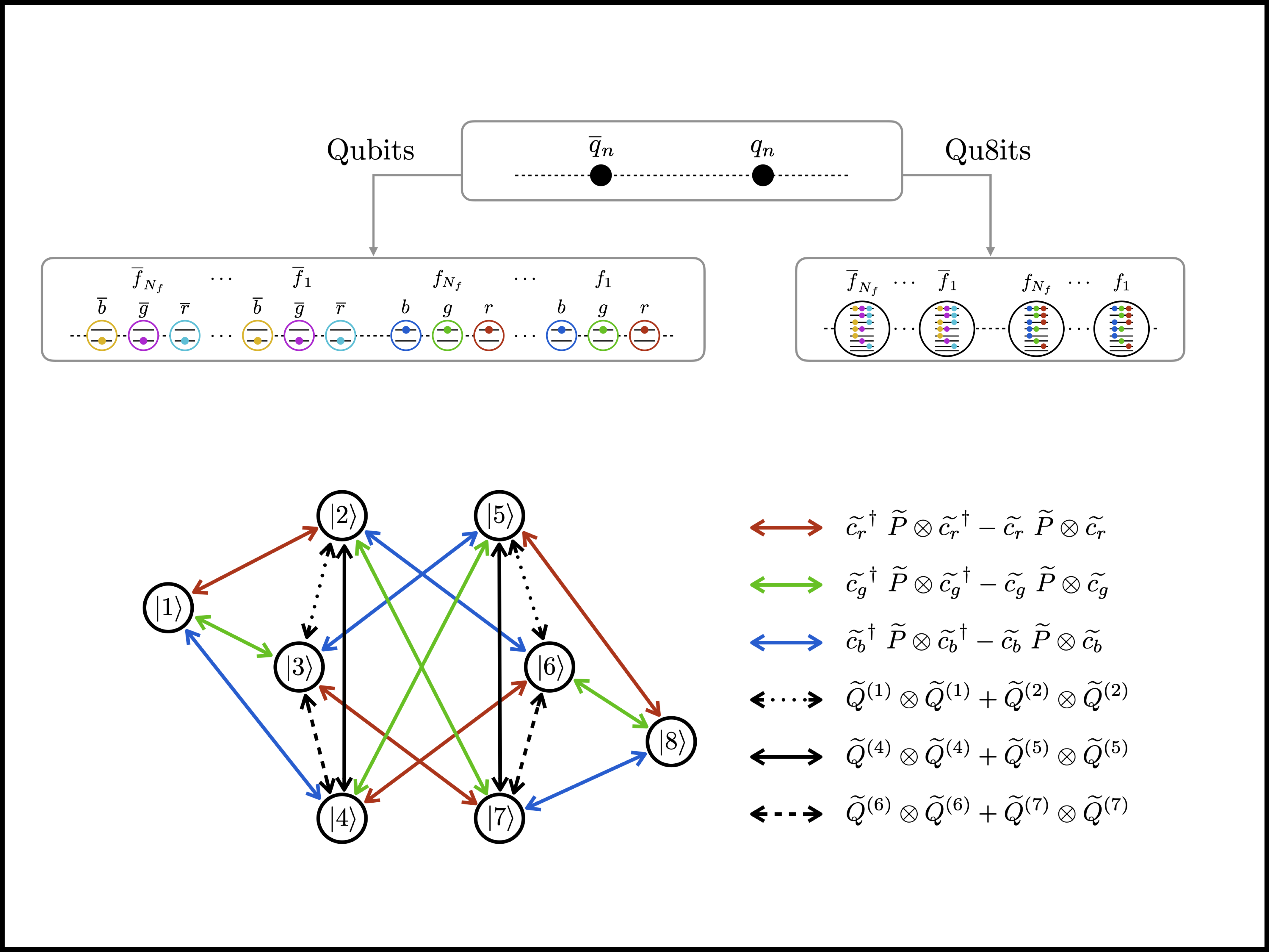
Qu8its for Quantum Simulations of Lattice Quantum Chromodynamics
Marc Illa, Caroline E. P. Robin, Martin J. Savage |
arXiv:2403.14537 [quant-ph], Phys.Rev.D 110, 014507 (2024).
We explore the utility of d = 8 qudits, qu8its, for quantum simulations of the dynamics of 1+1D
SU(3) lattice quantum chromodynamics, including a mapping for arbitrary numbers of flavors and
lattice size and a re-organization of the Hamiltonian for efficient time-evolution. Recent advances
in parallel gate applications, along with the shorter application times of single-qudit operations
compared with two-qudit operations, lead to significant projected advantages in quantum simulation
fidelities and circuit depths using qu8its rather than qubits. The number of two-qudit entangling
gates required for time evolution using qu8its is found to be more than a factor of five fewer than for
qubits. We anticipate that the developments presented in this work will enable improved quantum
simulations to be performed using emerging quantum hardware.
Multi-Body Entanglement and Information Rearrangement in Nuclear Many-Body Systems
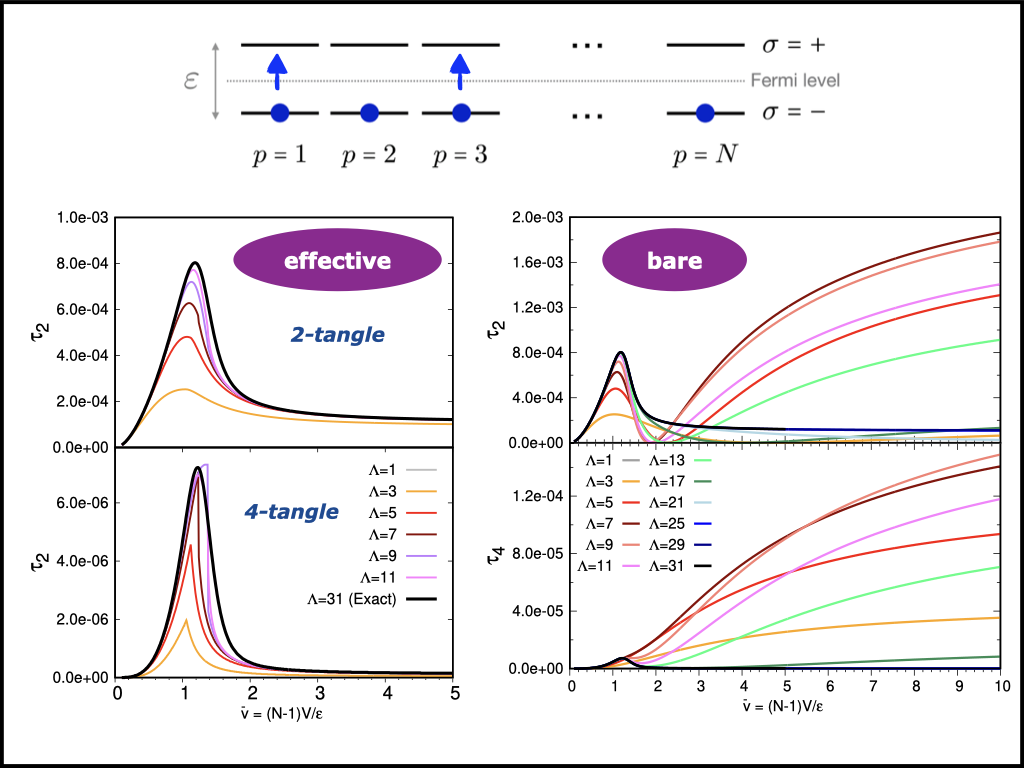
S. Momme Hengstenberg, Caroline E. P. Robin, Martin J. Savage |
arXiv:2306.16535 [nucl-th], Eur. Phys. J. A 59, 231 (2023)
The present work examines how effective-model-space calculations of nuclear many-body systems are able to rearrange and converge information and multi-particle entanglement.
To this aim we considered the LMG model as a demonstration, which allowed us to understand and shed light on the accelerated convergence of classical and quantum simulations found in our previous study in terms of entanglement point of view.
The method is based on a truncation of the Hilbert space together with a variational rotation of the relevant elementary degrees of freedom (qubits in this model), thereby defining an effective Hamiltonian.
The rotated qubits were found to provide effective DoF exhibiting strongly-suppressed and fast-converging bi- and multi-partite entanglement measures, such as entanglement entropy, mutual information and n-tangles, while largely capturing the exact results with small model spaces.
This work provides insights motivating future studies in nuclear many-body systems that are closer to nature, and future developments of entanglement-driven descriptions of nuclei.
Quantum Simulations of SO(5) Many-Fermion Systems using Qudits
Marc Illa, Caroline E. P. Robin, Martin J. Savage |
arXiv:2305.11941 [quant-ph], Phys. Rev. C 108, 064306 (2023)
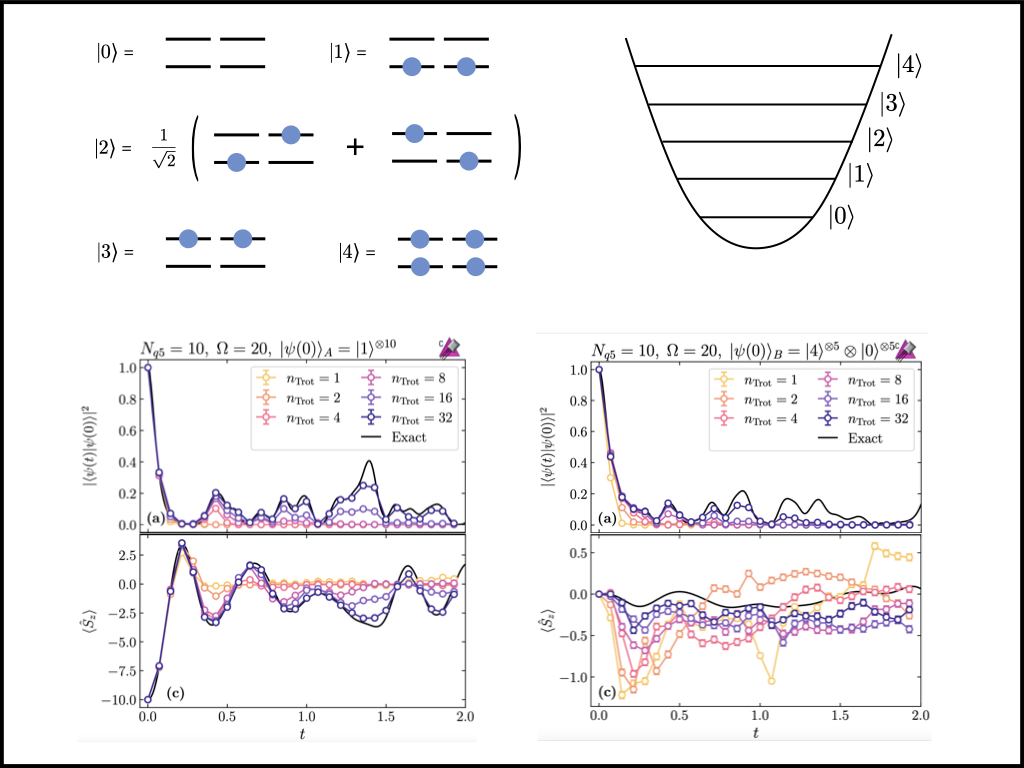 The structure and dynamics of quantum many-body systems are the result of a delicate interplay between underlying interactions, which leads to intricate entanglement structures. Despite this apparent complexity, symmetries emerge and have long been used to determine the relevant degrees of freedom and simplify classical descriptions of these systems.
In this paper, we explore the potential utility of quantum computers with arrays of qudits (d-level quantum systems) in simulating interacting fermionic systems with underlying symmetries, when the qudits can naturally map these relevant degrees of freedom.
As an example, we consider the Agassi model of fermions which is based on an underlying so(5) algebra, with subsystems which can be partitioned into pairs of modes with five basis states, naturally embedding in arrays of d=5 qudits (qu5its).
Classical noiseless simulations of the time evolution of systems of fermions embedded in up to twelve qu5its are performed using Google's cirq software.
We find advantages in using qudits, as opposed to qubits. specifically in lowering the required quantum resources and reducing anticipated errors that take the simulation out of the physical space. A previously unrecognized sign problem has been identified from Trotterization errors in time evolving high-energy excitations. This has implications for quantum simulations in high-energy and nuclear physics, specifically of fragmentation and highly inelastic, multi-channel processes.
The structure and dynamics of quantum many-body systems are the result of a delicate interplay between underlying interactions, which leads to intricate entanglement structures. Despite this apparent complexity, symmetries emerge and have long been used to determine the relevant degrees of freedom and simplify classical descriptions of these systems.
In this paper, we explore the potential utility of quantum computers with arrays of qudits (d-level quantum systems) in simulating interacting fermionic systems with underlying symmetries, when the qudits can naturally map these relevant degrees of freedom.
As an example, we consider the Agassi model of fermions which is based on an underlying so(5) algebra, with subsystems which can be partitioned into pairs of modes with five basis states, naturally embedding in arrays of d=5 qudits (qu5its).
Classical noiseless simulations of the time evolution of systems of fermions embedded in up to twelve qu5its are performed using Google's cirq software.
We find advantages in using qudits, as opposed to qubits. specifically in lowering the required quantum resources and reducing anticipated errors that take the simulation out of the physical space. A previously unrecognized sign problem has been identified from Trotterization errors in time evolving high-energy excitations. This has implications for quantum simulations in high-energy and nuclear physics, specifically of fragmentation and highly inelastic, multi-channel processes.
Quantum Simulations in Effective Model Spaces (I): Hamiltonian Learning-VQE using Digital Quantum Computers and Application to the Lipkin-Meshkov-Glick Model
Caroline Robin, Martin J. Savage |
arXiv:2301.05976 [quant-ph], Phys.Rev.C 108, 024313 (2023).
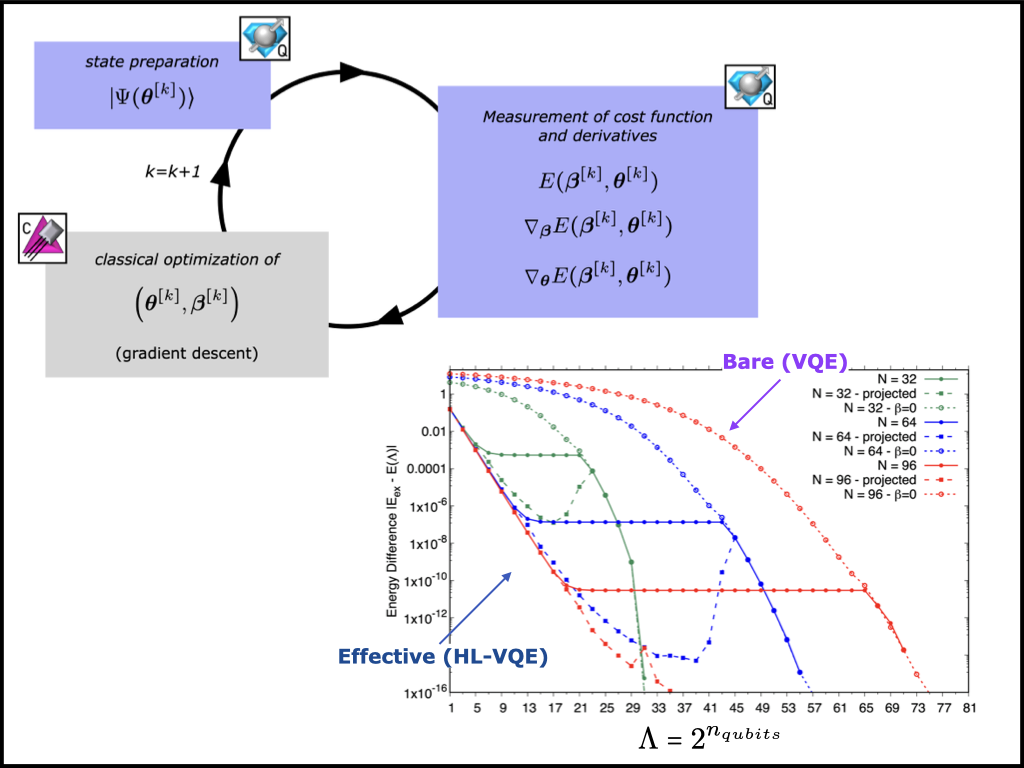 In this work we explored the utility of effective model spaces in quantum simulations of non-relativistic quantum many-body systems, considering the Lipkin-Meshkov-Glick model of interacting fermions as an example.
We introduced a new iterative hybrid-classical-quantum algorithm, Hamiltonian learning variational quantum eigensolver (HL-VQE), that simultaneously optimizes an effective Hamiltonian and the associated ground-state wavefunction.
HL-VQE is found to provide an exponential improvement in Lipkin-Meshkov-Glick model calculations, compared to a naive truncation without Hamiltonian learning, throughout a significant fraction of the Hilbert space.
Quantum simulations are performed to demonstrate the HL-VQE algorithm, using an efficient mapping where the number of qubits scales with the log of the size of the effective model space, rather than the particle number, allowing for the description of large systems with small quantum circuits. Implementations on IBM's QExperience quantum computers and simulators for 1- and 2-qubit effective model spaces are shown to provide accurate and precise results, reproducing classical predictions.
In this work we explored the utility of effective model spaces in quantum simulations of non-relativistic quantum many-body systems, considering the Lipkin-Meshkov-Glick model of interacting fermions as an example.
We introduced a new iterative hybrid-classical-quantum algorithm, Hamiltonian learning variational quantum eigensolver (HL-VQE), that simultaneously optimizes an effective Hamiltonian and the associated ground-state wavefunction.
HL-VQE is found to provide an exponential improvement in Lipkin-Meshkov-Glick model calculations, compared to a naive truncation without Hamiltonian learning, throughout a significant fraction of the Hilbert space.
Quantum simulations are performed to demonstrate the HL-VQE algorithm, using an efficient mapping where the number of qubits scales with the log of the size of the effective model space, rather than the particle number, allowing for the description of large systems with small quantum circuits. Implementations on IBM's QExperience quantum computers and simulators for 1- and 2-qubit effective model spaces are shown to provide accurate and precise results, reproducing classical predictions.
This work constitutes a step in the development of entanglement-driven quantum algorithms for the description of nuclear systems, that leverages the potential of noisy intermediate-scale quantum (NISQ) devices.
Entanglement Rearrangement in Self-Consistent Nuclear Structure Calculations
Caroline Robin, Martin J. Savage, Nathalie Pillet |
arXiv:2007.09157 [nucl-th], Phys.Rev.C 103, 034325 (2021).
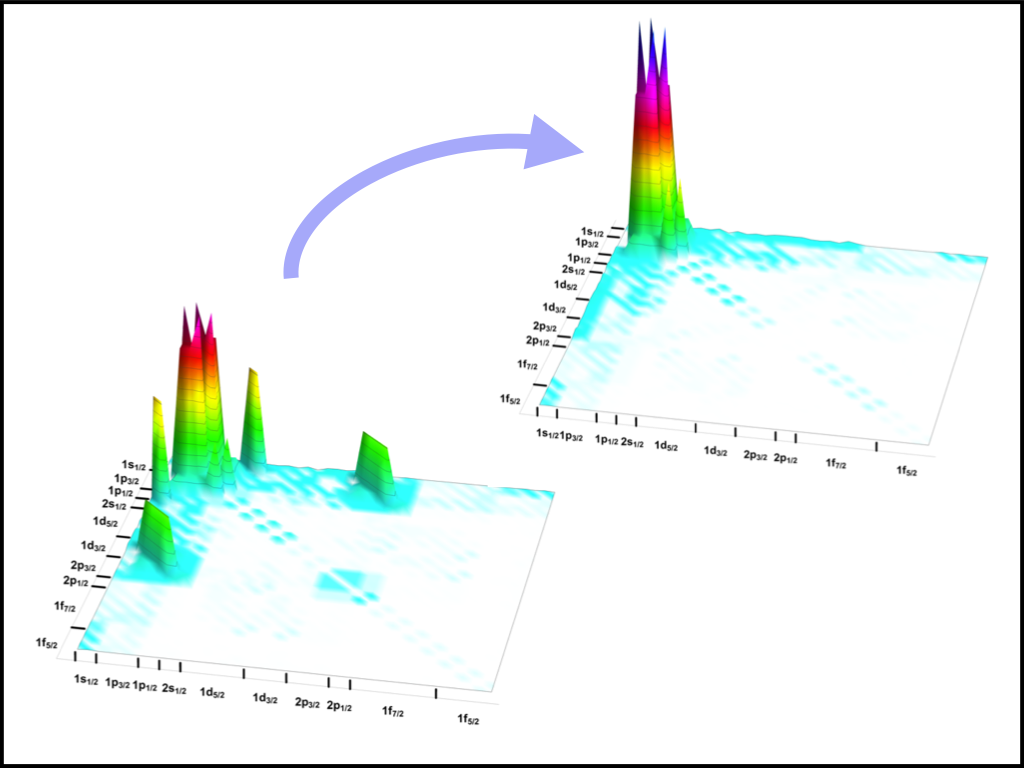
The goal of this work was to begin investigating the entanglement properties of nuclei from first-principle nuclear many-body calculations. We studied entanglement features of single-particle orbitals within the nuclear ground state of 4He and 6He using a chiral two-body interaction. The patterns of entanglement emerging from different single-particle bases were compared, and possible links with the convergence of ground state energies were explored.
Overall we found that orbitals derived from a variational principle (applied to the correlated ground state) display much more localized structures of entanglement within the basis, as compared to, for example, harmonic oscillator or Hartree-Fock orbitals. In particular, a core-valence structure clearly emerges from the full no-core calculation of 6He using the variational basis. The two-nucleon mutual information showed that this basis, which typically exhibits good convergence properties, effectively decouples the active and inactive spaces.
In the future, such studies may be useful to develop more efficient entanglement-based many-body schemes, and may have benefits for designing hybrid classical-quantum computations of nuclei.

 C. E. P. Robin |
C. E. P. Robin |
 I. Chernyshev, C. E. P. Robin and M. J. Savage |
I. Chernyshev, C. E. P. Robin and M. J. Savage |
 F. Brökemeier, S. M. Hengstenberg, J. W. Keeble, C. E. P. Robin, F. Rocco and M. J. Savage |
F. Brökemeier, S. M. Hengstenberg, J. W. Keeble, C. E. P. Robin, F. Rocco and M. J. Savage |
 Caroline Robin and Martin Savage |
Caroline Robin and Martin Savage |

 S. Momme Hengstenberg, Caroline E. P. Robin, Martin J. Savage |
S. Momme Hengstenberg, Caroline E. P. Robin, Martin J. Savage |
 The structure and dynamics of quantum many-body systems are the result of a delicate interplay between underlying interactions, which leads to intricate entanglement structures. Despite this apparent complexity, symmetries emerge and have long been used to determine the relevant degrees of freedom and simplify classical descriptions of these systems.
In this paper, we explore the potential utility of quantum computers with arrays of qudits (d-level quantum systems) in simulating interacting fermionic systems with underlying symmetries, when the qudits can naturally map these relevant degrees of freedom.
As an example, we consider the Agassi model of fermions which is based on an underlying so(5) algebra, with subsystems which can be partitioned into pairs of modes with five basis states, naturally embedding in arrays of d=5 qudits (qu5its).
Classical noiseless simulations of the time evolution of systems of fermions embedded in up to twelve qu5its are performed using Google's cirq software.
We find advantages in using qudits, as opposed to qubits. specifically in lowering the required quantum resources and reducing anticipated errors that take the simulation out of the physical space. A previously unrecognized sign problem has been identified from Trotterization errors in time evolving high-energy excitations. This has implications for quantum simulations in high-energy and nuclear physics, specifically of fragmentation and highly inelastic, multi-channel processes.
The structure and dynamics of quantum many-body systems are the result of a delicate interplay between underlying interactions, which leads to intricate entanglement structures. Despite this apparent complexity, symmetries emerge and have long been used to determine the relevant degrees of freedom and simplify classical descriptions of these systems.
In this paper, we explore the potential utility of quantum computers with arrays of qudits (d-level quantum systems) in simulating interacting fermionic systems with underlying symmetries, when the qudits can naturally map these relevant degrees of freedom.
As an example, we consider the Agassi model of fermions which is based on an underlying so(5) algebra, with subsystems which can be partitioned into pairs of modes with five basis states, naturally embedding in arrays of d=5 qudits (qu5its).
Classical noiseless simulations of the time evolution of systems of fermions embedded in up to twelve qu5its are performed using Google's cirq software.
We find advantages in using qudits, as opposed to qubits. specifically in lowering the required quantum resources and reducing anticipated errors that take the simulation out of the physical space. A previously unrecognized sign problem has been identified from Trotterization errors in time evolving high-energy excitations. This has implications for quantum simulations in high-energy and nuclear physics, specifically of fragmentation and highly inelastic, multi-channel processes.  In this work we explored the utility of effective model spaces in quantum simulations of non-relativistic quantum many-body systems, considering the Lipkin-Meshkov-Glick model of interacting fermions as an example.
We introduced a new iterative hybrid-classical-quantum algorithm, Hamiltonian learning variational quantum eigensolver (HL-VQE), that simultaneously optimizes an effective Hamiltonian and the associated ground-state wavefunction.
HL-VQE is found to provide an exponential improvement in Lipkin-Meshkov-Glick model calculations, compared to a naive truncation without Hamiltonian learning, throughout a significant fraction of the Hilbert space.
Quantum simulations are performed to demonstrate the HL-VQE algorithm, using an efficient mapping where the number of qubits scales with the log of the size of the effective model space, rather than the particle number, allowing for the description of large systems with small quantum circuits. Implementations on IBM's QExperience quantum computers and simulators for 1- and 2-qubit effective model spaces are shown to provide accurate and precise results, reproducing classical predictions.
In this work we explored the utility of effective model spaces in quantum simulations of non-relativistic quantum many-body systems, considering the Lipkin-Meshkov-Glick model of interacting fermions as an example.
We introduced a new iterative hybrid-classical-quantum algorithm, Hamiltonian learning variational quantum eigensolver (HL-VQE), that simultaneously optimizes an effective Hamiltonian and the associated ground-state wavefunction.
HL-VQE is found to provide an exponential improvement in Lipkin-Meshkov-Glick model calculations, compared to a naive truncation without Hamiltonian learning, throughout a significant fraction of the Hilbert space.
Quantum simulations are performed to demonstrate the HL-VQE algorithm, using an efficient mapping where the number of qubits scales with the log of the size of the effective model space, rather than the particle number, allowing for the description of large systems with small quantum circuits. Implementations on IBM's QExperience quantum computers and simulators for 1- and 2-qubit effective model spaces are shown to provide accurate and precise results, reproducing classical predictions. 







